Funciones
Concepto.
Es una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto. Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):
| ... | −2 → +4, | −1 → +1, | ±0 → ±0, | |
| +1 → +1, | +2 → +4, | +3 → +9, | ... |
Gráfica de una Función.

es la representación gráfica de la correspondencia entre los elementos del conjunto dominio y los del conjunto imagen. Es el conjunto formado por todos los pares ordenados (x, f(x)) de la función f; es decir, como un subconjunto del producto cartesiano X×Y.
Las únicas funciones que se pueden trazar de forma completa son las de una sola variable, con un sistema de coordenadas cartesianas, donde cada abscisa representa un valor de la variable del dominio y cada ordenada representa el valor correspondiente del conjunto imagen. Si la función es continua, entonces la gráfica formará una línea recta o curva.
Tipos de funciones.
- Función lineal.
una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:
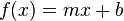
donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y.
- Funcion Constante.
En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable. Se la representa de la forma:
- Función Cuadrática.
En matemáticas, una función cuadrática o función de segundo grado es una función polinómica definida como:

en donde a, b y c son números reales (constantes) y a es distinto de 0.
La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso contrario.

- Función racional.
En matemáticas, una función racional es una función que puede ser expresada de la forma:
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.
Funcion racional de grado 2
Función racional de grado 3:
- Función Exponencial.
a función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
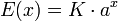
siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico de exponenciales, todas ellas similares, que dependen de la base a que utilicen.
En términos mucho más generales, una función real E(x) se dice que es del tipo exponencial en base a si tiene la forma
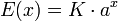
Bachiller:
Daniel tovar
Exp. 26778







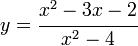










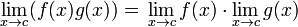




 .
. como el límite que tiende a infinito y
como el límite que tiende a infinito y  al límite cuando tiende a 0; y no al número 0):
al límite cuando tiende a 0; y no al número 0):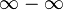

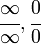



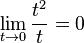

 ,
entonces
,
entonces




 y
y  , viene dada por la fórmula:
, viene dada por la fórmula:

 y que la derivada de
y que la derivada de  es precisamente
es precisamente  .
.  viene dada por la fórmula:
viene dada por la fórmula: 
